log_coffee!
- Feb 19, 2026 The Rust Strawberry test
- Jun 21, 2023 Sweet Jesus, Pooh! That’s Not Honey! - You’re Eating Recursion!
- Apr 29, 2023 Why u so mean?
- Mar 25, 2023 Lindenmayer systems
Archive
An archive of previous blog posts written in Medium
- Nov 05, 2019 Visualization
- Aug 31, 2018 Fractals
- Sep 19, 2016 The center of the Universe is not a black hole. It’s the opposite
- Aug 07, 2016 Choosing a good hash function
- Jun 25, 2016 How I downloaded Big Bang Theory Season 9 in my unstable network
The Rust Strawberry test
One fine day at work, I came across a piece of code in Rust that looked like this:
fn main() {
// Will this panic or not?
let s : Vec<u8> = vec![0u8; 32];
println!("{:?}", &s[1..=0]);
}Initially, I thought, Oh no, this will panic! So, I threw this sample into the Rust playground to test it out. And… it returned an empty slice!!! NO PANIC.
Let’s dig into why. &s[1..=0] breaks down into the SliceIndex implementation for RangeInclusive:
#![allow(unused)]
fn main() {
unsafe impl<T> const SliceIndex<[T]> for ops::RangeInclusive<usize> {
type Output = [T];
#[inline]
fn get(self, slice: &[T]) -> Option<&[T]> {
if *self.end() == usize::MAX { None } else { self.into_slice_range().get(slice) }
}
#[inline]
fn get_mut(self, slice: &mut [T]) -> Option<&mut [T]> {
if *self.end() == usize::MAX { None } else { self.into_slice_range().get_mut(slice) }
}
#[inline]
unsafe fn get_unchecked(self, slice: *const [T]) -> *const [T] {
// SAFETY: the caller has to uphold the safety contract for `get_unchecked`.
unsafe { self.into_slice_range().get_unchecked(slice) }
}
#[inline]
unsafe fn get_unchecked_mut(self, slice: *mut [T]) -> *mut [T] {
// SAFETY: the caller has to uphold the safety contract for `get_unchecked_mut`.
unsafe { self.into_slice_range().get_unchecked_mut(slice) }
}
#[inline]
fn index(self, slice: &[T]) -> &[T] {
...
if end < len {
end = end + 1;
...
}
slice_index_fail(start, end, slice.len())
}
#[inline]
fn index_mut(self, slice: &mut [T]) -> &mut [T] {
...
if end < len {
end = end + 1;
...
}
slice_index_fail(start, end, slice.len())
}
}In this implementation, index and index_mut handle the end + 1, while the rest delegate it to into_slice_range, which handles it properly as well:
#![allow(unused)]
fn main() {
impl RangeInclusive<usize> {
#[inline]
pub(crate) const fn into_slice_range(self) -> Range<usize> {
let exclusive_end = self.end + 1;
let start = if self.exhausted { exclusive_end } else { self.start };
start..exclusive_end
}
}
}So, in short, despite my intuition, this code is safe. ✅
But what do the LLMs think?
Well, the results reminded me of the infamous Strawberry incident. For the sake of uniformity, all prompts were tested using free accounts on their respective platforms.
| LLM | Panic or No Panic |
|---|---|
| ChatGPT GPT 5.2 | ✅ Panic |
| Claude Sonnet 4.5 | ✅ Panic |
| Claude Sonnet 4.6 | ❌ No Panic |
| DeepSeek v3.2 | ✅ Panic |
| Gemini 3 Pro | ✅ Panic |
| Gemini 3.1 Pro | ❌ No Panic |
| Grok | ✅ Panic |
| Kimi K2.5 | ✅ Panic |
ChatGPT GPT 5.2 - Panic!
Yes — this will panic at runtime.
Why?
You created:
#![allow(unused)]
fn main() {
let s: Vec<u8> = vec![0u8; 32];
}So s has length 32.
Then you slice it with:
#![allow(unused)]
fn main() {
&s[1..=0]
}This is an inclusive range from index 1 to index 0.
That means:
- start = 1
- end = 0
- inclusive range (
..=)
In Rust, slicing requires:
start <= end + 1 (for inclusive ranges this effectively means start <= end)
But here:
1 > 0
So the range is invalid.
What happens?
Rust performs bounds checking at runtime for slices. Since the start index is greater than the end index, it triggers:
thread 'main' panicked at 'slice index starts at 1 but ends at 0'
Important Detail
Even though both indices (0 and 1) are individually valid indices for a 32-element vector, the range itself is invalid, which causes the panic.
Contrast Example (This does NOT panic)
#![allow(unused)]
fn main() {
&s[1..1] // empty slice, valid
}This produces an empty slice because the start equals the end.
Final Answer
✅ Yes, it panics at runtime because the slice range 1..=0 is invalid (start > end).
Claude Sonnet 4.5 - Panic!
This code will panic at runtime.
Here’s why: &s[1..=0] is an inclusive range (notice the =), which means it’s trying to create a slice from index 1 up to and including index 0. This is logically impossible since you can’t have a range where the start index (1) is greater than the end index (0).
When you use an inclusive range start..=end, Rust requires that start <= end. In this case, 1 <= 0 is false, so the indexing operation will panic with an error like:
thread 'main' panicked at 'range start index 1 out of range for slice of length 0'
or similar message about the range being invalid.
If you wanted an empty slice, you could use:
&s[0..0](exclusive range, valid)&s[1..1](exclusive range, valid)
But &s[1..=0] is invalid because inclusive ranges cannot have start > end.
Claude Sonnet 4.6 - no Panic!
This will not panic — it prints [].
The range 1..=0 is an empty range (since the end is less than the start in an inclusive range). Rust’s slice indexing accepts empty ranges like this as long as the bounds are within the valid index range for the slice, and 1 is a valid index into a 32-element vector.
If you tried 1..=0 on an empty vector or 33..=32 (out of bounds), that would panic. But here, 1 is within bounds, so Rust happily returns an empty slice.
You can verify:
fn main() {
let s: Vec<u8> = vec![0u8; 32];
println!("{:?}", &s[1..=0]); // prints: []
}Interestingly, 0..0 (exclusive) also gives [], but 2..=1 would also work fine for the same reason — the bounds are checked individually against the slice length, not against each other.
DeepSeek v3.2 - Panic!
Let’s analyze this code step by step:
fn main() {
// Will this panic or not?
let s : Vec<u8> = vec![0u8; 32];
println!("{:?}", &s[1..=0]);
}This code will panic at runtime.
Explanation:
The slice &s[1..=0] is trying to create a range from index 1 to index 0 (inclusive). This is an invalid range because:
1..=0means “from 1 up to and including 0”- This is impossible since the start index (1) is greater than the end index (0)
When Rust encounters an invalid range like this during indexing operations, it will panic with a message similar to:
thread 'main' panicked at 'slice index starts at 1 but ends at 0'
Important Note:
Even though the vector has 32 elements (indices 0-31), the slice operation fails before it even checks if the indices are within bounds. The range itself is invalid because start > end for an inclusive range.
The only non-panicking behavior with invalid ranges occurs with exclusive ranges (..) where an empty range is valid (e.g., &s[1..1] would give an empty slice without panicking).
Gemini 3 Pro - Panic!
Google rolled out Gemini 3.1 Pro as I was writing this, so Gemini 3 Pro replication is done on AI studio.
Yes, this code will panic at runtime.
Specifically, it will panic with a message similar to:
thread 'main' panicked at 'slice index starts at 1 but ends at 0', src/main.rs:4:20
Why?
When you slice a vector (or array) in Rust, the range must be valid.
- Exclusive Range (
start..end): The slice is empty ifstart == end. It panics ifstart > end. - Inclusive Range (
start..=end): This syntax implies that the slice must contain indices fromstartup to and includingend.
In your code, you requested 1..=0. Since the start index (1) is greater than the end index (0), Rust considers this an invalid range for slicing and panics to prevent logic errors.
If you wanted an empty slice starting at 1, you should use an exclusive range:
#![allow(unused)]
fn main() {
&s[1..1] // This is valid (empty slice)
}Gemini 3.1 Pro - no Panic!
The short answer: No, it will not panic.
While it looks like you are trying to slice “backward” (from index 1 to 0), Rust handles this specific case gracefully because of how inclusive ranges work.
Why it works
In Rust, an inclusive range start..=end is considered empty if start > end. When you slice a Vec or a slice with an empty range, Rust returns an empty slice rather than panicking, provided the starting index is within the bounds of the container.
-
The Container:
shas a length of 2 (indices 0 and 1). -
The Slice:
&s[1..=0] -
The start index
1is less than or equal to the length of the vector, so the starting point is valid. -
Since
1 > 0, the range1..=0contains no elements. -
The Result: You get an empty slice:
[].
Comparison: When would it panic?
To give you some perspective, here is where the code would break:
| Scenario | Code | Result | Why? |
|---|---|---|---|
| Valid Empty Slice | &s[1..=0] | [] | Start index is within bounds; range is empty. |
| Out of Bounds | &s[3..=0] | Panic | The start index 3 is greater than the length 2. |
| Inclusive vs. Exclusive | &s[0..=2] | Panic | Index 2 is out of bounds for an inclusive range (max index is 1). |
Output
If you run your code, the console will print:
#![allow(unused)]
fn main() {
[]
}Would you like to see how this behavior changes if you use an exclusive range like &s[1..0], or should we look at how to safely handle slicing with the .get() method?
Grok - Panic!
Yes, this code will panic.
The expression &s[1..=0] creates an invalid slice range in Rust.
Why it panics
In Rust, for a range start..=end (inclusive range):
- it is only valid when
start ≤ end - when
start > end, the range is empty — but only if you use..=with integers that satisfy start ≤ end + 1
But here:
#![allow(unused)]
fn main() {
1 ..= 0
}→ 1 > 0
→ this is an invalid inclusive range
Rust does not allow creating an inclusive range where the start is greater than the end — it panics at runtime when you try to use it in a slice.
Quick comparison
#![allow(unused)]
fn main() {
&vec[1..0] // this is OK → empty slice (non-inclusive)
&vec[1..=0] // this PANICS (inclusive, but 1 > 0)
}What actually happens
#![allow(unused)]
fn main() {
let s: Vec<u8> = vec![0u8; 32];
println!("{:?}", &s[1..=0]); // ← panic here
}Output:
thread 'main' panicked at 'range start is greater than end'
(or very similar message depending on Rust version)
Correct ways to write an empty slice
#![allow(unused)]
fn main() {
&s[1..1] // classic way, always empty
&s[5..5]
&s[..0] // from beginning to 0 → empty
&vec![0u8;32][10..=9] // this also panics (same reason)
}So short answer:
Yes — your code panics.
Because 1..=0 is an invalid inclusive range.
Want to see many ways to get empty slices safely? 😄
Kimi K2.5 - Panic!
This is an interesting Rust question about slice indexing behavior. Let me analyze this code without needing any tools.
Analysis
The code creates a vector of 32 zeros, then tries to print &s[1..=0].
The key question: Will this panic or not?
Answer: Yes, this will panic! 🚨
Here’s why:
The Range 1..=0 (Inclusive Range)
In Rust, range bounds have specific rules:
start..=endis an inclusive range- The critical rule: The
startmust be ≤endfor the range to be valid
When you write 1..=0:
- Start = 1
- End = 0 (inclusive)
Since 1 > 0, this violates the range invariant that start ≤ end.
What Happens
#![allow(unused)]
fn main() {
let s: Vec<u8> = vec![0u8; 32];
println!("{:?}", &s[1..=0]); // PANIC!
}Panic message:
thread 'main' panicked at 'slice index starts at 1 but ends at 0'
Why Not an Empty Slice?
You might think “1 to 0 is just empty,” but Rust’s slice indexing doesn’t work that way. The bounds are checked before considering what elements would be selected. The range 1..=0 is considered invalid because:
- Start (1) > End (0)
- This is always an error, regardless of the vector’s contents
Contrast with Valid Empty Ranges
These would not panic (they produce empty slices):
#![allow(unused)]
fn main() {
&s[0..0] // start == end, valid empty range
&s[1..1] // start == end, valid empty range
&s[32..32] // start == end == len, valid empty range
&s[1..0] // wait... this also panics! (exclusive range with start > end)
}Even 1..0 (exclusive) panics for the same reason.
Summary
| Expression | Result |
|---|---|
s[0..0] | ✅ Empty slice &[] |
s[1..1] | ✅ Empty slice &[] |
s[1..0] | ❌ Panic (start > end) |
s[1..=0] | ❌ Panic (start > end) |
The panic occurs because Rust validates that range bounds are logically ordered before applying them to the slice.
Sweet Jesus, Pooh! That’s Not Honey! - You’re Eating Recursion!
Most of the time, using Rust is just bliss. But today, it took us for a ride. We were reviewing some code (simplified for the blog) and stumbled upon a nested enum that looked like this
#![allow(unused)]
fn main() {
#[derive(Debug)]
enum Tree {
Leaf,
SubTree(Vec<Tree>),
}
}Assume Leaf is a placeholder to hold some data and thus the enum allows you to create a Rose tree. Now, we have a function create_nested_tree that accepts a single parameter depth as input and creates a flat Tree with depth depth and a Leaf at the end.
fn create_nested_tree(depth : i32) -> Tree {
let mut tree = Tree::Leaf;
for _ in 0..depth {
tree = Tree::SubTree(vec![tree]);
}
tree
}
fn main() {
println!("{:#?}", create_nested_tree(5));
}
This would produce the following output.
SubTree(
[
SubTree(
[
SubTree(
[
SubTree(
[
SubTree(
[
Leaf,
],
),
],
),
],
),
],
),
],
)
As one behaves when they see deeply nested structures, We tried giving a large depth (50_000) to see what happens.
fn main() {
println!("{:#?}", create_nested_tree(50_000));
}And there we go,
thread 'main' has overflowed its stack
fatal runtime error: stack overflow
Aborted (core dumped)
Initially, we immediately suspected the fmt::Debug hitting a recursive call and was causing the stack overflow. So, we removed the println! from main and included a println! in create_nested_tree before returning to value to isolate the issue. (What’s a debugger?)
Note that the function
create_nested_treeiteratively creates the nestedTreeand there shouldn’t be any concern of stack overflow.
#[derive(Debug)]
enum Tree {
Leaf,
SubTree(Vec<Tree>),
}
fn create_nested_tree(depth : i32) -> Tree {
let mut tree = Tree::Leaf;
for _ in 0..depth {
tree = Tree::SubTree(vec![tree]);
}
println!("End of create_nested_tree");
tree
}
fn main() {
let _ = create_nested_tree(50_000);
}But to our surprise,
End of create_nested_tree
thread 'main' has overflowed its stack
fatal runtime error: stack overflow
Aborted (core dumped)
There is no operation happening after returning the value and the code still stack overflows after the return. To debug, we created the MIR of our code and looked at create_nested_tree.
cargo rustc -- --emit=mir
fn create_nested_tree(_1: i32) -> Tree {
debug depth => _1; // in scope 0 at src/main.rs:7:23: 7:28
let mut _0: Tree; // return place in scope 0 at src/main.rs:8:9: 8:17
// for loop logic (removed for brevity)
bb10: {
_29 = const false; // scope 1 at src/main.rs:13:5: 13:9
_29 = const false; // scope 0 at src/main.rs:14:1: 14:2
return; // scope 0 at src/main.rs:14:2: 14:2
}
bb11 (cleanup): {
resume; // scope 0 at src/main.rs:7:1: 14:2
}
bb12 (cleanup): {
drop(_0) -> bb11; // scope 0 at src/main.rs:14:1: 14:2
}
bb13 (cleanup): {
switchInt(_29) -> [false: bb11, otherwise: bb12]; // scope 0 at src/main.rs:14:1: 14:2
}
}
And there is our culprit block bb12. Once the variable _0 ie tree in our code goes out of scope (return to main), the code invokes cleanup of memory of local variables and tries to drop _0.
But why would dropping a value cause a stack overflow? If not anything, we are trying to free memory. This is where the beauty of the Rust implementation and my loss of hair kicks in
When an initialized variable in Rust goes out of scope or a temporary is no longer needed its destructor is run. The assignment also runs the destructor of its left-hand operand, unless it’s an uninitialized variable. If a struct variable has been partially initialized, only its initialized fields are dropped. The destructor of a type consists of
- Calling its std::ops::Drop::drop method, if it has one.
- Recursively running the destructor of all of its fields.
- The fields of a struct, tuple, or enum variant are dropped in declaration order.
- The elements of an array or owned slice are dropped from the first element to the last.
- The captured values of a closure are dropped in an unspecified order.
- Trait objects run the destructor of the underlying type.
- Other types don’t result in any further drops.
Source: Destructors
Following the description of Destructor, since we don’t have our Drop implementation, it tries to drop the values Leaf and SubTree in the enum. However, the nested nature of the enum recursively places drop calls on the stack and hence causes the stack overflow
Finally an explanation, but how do we solve this? By implementing our own Drop implementation which isn’t recursive.
#![allow(unused)]
fn main() {
impl Drop for Tree {
fn drop(&mut self) {
let mut stack = vec![*self];
while let Some(mut node) = stack.pop() {
match node {
Tree::Leaf => {}
Tree::SubTree(ref mut children) => {
stack.extend(children.drain(..));
}
}
// This is safe to drop
let _ = std::mem::replace(&mut node, Tree::Leaf);
}
}
}
}Rough logic behind the code
- Create our stack (ironic) and push the entire tree.
- Keep popping the values of the stack until its empty
- If the node is a
Leaf, you don’t need to do anything since Rust can drop it safely. - If the node is a
SubTree(Vec<Tree>), we collect all the subtrees in the vec and push them into the stack. This is achieved bychildren.drain(..). Now, we have to makenodesafe to drop. Luckily, Rust saves us again here, since it allocates the same amount of memory for each value type in anenumand so we can easily replace the value atnodewith aTree::Leaf
- If the node is a
Given this, when the stack is empty, all references of Tree::SubTree would have been replaced by Tree::Leaf and the tree would be safe to drop without any recursion. Or so I thought.
error[E0507]: cannot move out of `*self` which is behind a mutable reference
--> src/main.rs:9:30
|
9 | let mut stack = vec![*self];
| ^^^^^ move occurs because `*self` has type `Tree`, which does not implement the `Copy` trait
Couple of things to unpack here,
- We can’t do
#[derive(Copy, Clone)]since we have a Vec which does not implement Copy (as it rightfully should). - Should we even implement Copy here? Can I do something else to make it work?
Luckily yes, by using a wrapper struct we can get out of this issue.
#![allow(unused)]
fn main() {
#[derive(Debug)]
enum Tree {
Leaf,
SubTree(Vec<Tree>),
}
#[derive(Debug)]
struct Head(Tree);
}Now we can implement Drop for the wrapper Head in the same way and adapt our create_nested_tree slightly,
#![allow(unused)]
fn main() {
impl Drop for Head {
fn drop(&mut self) {
// We can solve the *self issue here by taking
// advantage of Rust allocating the same
// amount of memory for each value of the
// enum and thus swapping self.0 with
// `Head(Tree::Leaf)` allows a safe drop.
let mut tree = Tree::Leaf;
std::mem::swap(&mut self.0, &mut tree);
// Now we proceed to drop the bulk of the tree
// as we implemented before.
let mut stack = vec![tree];
while let Some(mut node) = stack.pop() {
match node {
Tree::Leaf => {}
Tree::SubTree(ref mut children) => {
stack.extend(children.drain(..));
}
}
let _ = std::mem::replace(&mut node, Tree::Leaf);
}
}
}
fn create_nested_tree(depth: i32) -> Head {
let mut tree = Tree::Leaf;
for _ in 0..depth {
tree = Tree::SubTree(vec![tree]);
}
Head(tree) // returning Head(Tree) instead of Tree
}
}Our new tree now looks like this
Head(
SubTree(
[
SubTree(
[
SubTree(
[
SubTree(
[
SubTree(
[
Leaf,
],
),
],
),
],
),
],
),
],
),
)
And finally our working code. You can try running it yourself with the ▶ button at the top and feel the relief.
#[derive(Debug)]
enum Tree {
Leaf,
SubTree(Vec<Tree>),
}
#[derive(Debug)]
struct Head(Tree);
impl Drop for Head {
fn drop(&mut self) {
let mut current = Tree::Leaf;
std::mem::swap(&mut self.0, &mut current);
let mut stack = vec![current];
while let Some(mut node) = stack.pop() {
match node {
Tree::Leaf => {}
Tree::SubTree(ref mut children) => {
stack.extend(children.drain(..));
}
}
let _ = std::mem::replace(&mut node, Tree::Leaf);
}
}
}
fn create_nested_tree(depth: i32) -> Head {
let mut tree = Tree::Leaf;
for _ in 0..depth {
tree = Tree::SubTree(vec![tree]);
}
Head(tree)
}
fn main() {
let _ = create_nested_tree(50_000);
println!("End of program");
}Fin. Guess I will have some 🦀 soup now
Update (23/06/2023)
After sitting on it for a while, we can actually do it without a wrapper.
#[derive(Debug)]
enum Tree {
Leaf,
SubTree(Vec<Tree>),
}
impl Drop for Tree {
fn drop(&mut self) {
match self {
Tree::Leaf => {}
Tree::SubTree(ref mut children) => {
let mut stack = vec![];
stack.extend(children.drain(..));
while let Some(mut node) = stack.pop() {
match node {
Tree::Leaf => {}
Tree::SubTree(ref mut children) => {
stack.extend(children.drain(..));
}
}
let _ = std::mem::replace(&mut node, Tree::Leaf);
}
}
}
}
}
fn create_nested_tree(depth: i32) -> Tree {
let mut tree = Tree::Leaf;
for _ in 0..depth {
tree = Tree::SubTree(vec![tree]);
}
tree
}
fn main() {
let _ = create_nested_tree(50_000);
println!("End of program");
}I didn’t deserve the 🦀 soup
Benchmarking
Since we have two implementations now, I wrote a small benchmark to test which one is actually performant
#![allow(unused)]
fn main() {
#[bench]
fn bench_drop_nested_tree(b: &mut Bencher) {
b.iter(|| {
for i in 0..100 {
let _ = create_nested_tree(i * 1000);
}
});
}
}- Without the wrapper
running 1 test
test tests::bench_drop_nested_tree ... bench: 245,870,757 ns/iter (+/- 16,996,363)
test result: ok. 0 passed; 0 failed; 0 ignored; 1 measured; 0 filtered out; finished in 73.85s
- With the wrapper Winner!
running 1 test
test tests::bench_drop_nested_tree ... bench: 165,135,733 ns/iter (+/- 25,180,926)
test result: ok. 0 passed; 0 failed; 0 ignored; 1 measured; 0 filtered out; finished in 48.66s
Why u so mean?
For a quadratic equation of the form \( x^2 + Bx + C = 0\), the roots of the equation is given by \[\frac{-B \pm \sqrt{B^2 - 4C}}{2}\] where
- sum of the roots = \(-B \)
- product of the roots = \(C\)
This is the representation everyone is most familiar with and widely used in high school. However, recently another representation has been proposed which offers much more intuition and further simplifies the equation.
Let the Arithmetic Mean of the roots be \( M = -B / 2\). Simplifying the roots, we have \[\frac{-B \pm \sqrt{B^2 - 4C}}{2}\] \[(-B/2) \pm \sqrt{B^2/4 - 4C/4}\] \[(-B/2) \pm \sqrt{(-B/2)^2 - C}\] \[M \pm \sqrt{M^2 - C}\]
This representation for roots is much simpler, as one needs to just evaluate the mean in the beginning to solve the roots of the equation.
Why?
Since the roots are equidistant from their mean, let’s represent the roots as \(M + u\) and \(M - u\) Hence, product of the roots \[C = (M + u)(M-u)\] \[C = M^2 - u^2\] \[u^2 = M^2 - C\] \[u = \sqrt{M^2 - C}\] Substituting \(u\) in the roots, we have the roots \(M + \sqrt{M^2 - C}\) and \(M - \sqrt{M^2 - C}\)
An interesting result that is much more obvious this way. If the roots are real, then \[M^2 - C \gt 0\] \[M \gt \sqrt{C}\] \[M \gt GM \] where GM is the geometric mean of roots given by \(\sqrt{C}\)
Credits to Po-Shen Loh for this improved and intuitive representation.
Lindenmayer systems
A Lindemayer system or LSystem for short consists of an alphabet of symbols that can be used to make strings, a collection of production that expand each symbol into some larger string of symbols, an initial “axiom” string from which to begin construction, and a mechanism for translating the generated strings into geometric structures.
A few years back, I built a rudimentary website to extrapolate a few known LSystems in pure JS. However, presently I have been getting more comfortable with Rust 🦀 and explored rebuilding it with Rust and wasm-bindgen to get better performance for tougher iterations.
Website - vsekar.me/LSystems/
Repository - github.com/Spockuto/LSystems/
Now let’s explore how an axiom, a set of rules, and an angle can be developed into this beautiful fern

Step 0 - Define the LSystem
For Barnsley Fern, the LSystem is defined as follows
Axiom : X
Rules :
- X -> F-[[X]+X]+F[+FX]-X
- F -> FF
Angle : 22.5
This translates into the following for our Rust implementation.
#![allow(unused)]
fn main() {
lazy_static! {
static ref BARNSLEY_FERN: LSystem = LSystem {
variables: "XF",
axiom: "X",
rules: vec![
('X', "F-[[X]+X]+F[+FX]-X"),
('F', "FF"),
]
.into_iter()
.collect(),
angle: 22.5,
max_rounds: 8,
};
}
}- variables : These are the identifiers that will be considered during building the sequence. Others will be skipped.
- axiom : The initial sequence
- rules : Expansion rules for each identifier
- angle : Explained later
- max_rounds - Implementation detail. Maximum number of supported iterations before running out of heap memory.
Step 1 - Generate the sequence
Once the LSystem is defined, we can build the drawing sequence. Iterations define the number of rounds the sequence will be expanded using the given rules. The higher the iteration, the better defined the picture is.
#![allow(unused)]
fn main() {
/// Generate the Turtle graphics sequence for given iterations
pub fn expand(&self, iterations: u32) -> String {
// panic if given iterations are greater than the accepted limit.
if iterations > self.0.max_rounds {
panic!("Max limit reached");
}
let mut sequence = String::new();
for i in 0..iterations {
if i == 0 {
// First iteration is the axiom
sequence.insert_str(0, self.0.axiom);
} else {
let sequence_copy = sequence.to_string();
let mut insert_index = 0;
for identifier in sequence_copy.chars() {
// Skip if the variable in sequence doesn't have a rule
if !self.0.variables.contains(identifier) {
insert_index += 1;
continue;
}
// Expand the sequence based on the rule
let rule = self.0.rules.get(&identifier).unwrap();
sequence.remove(insert_index);
sequence.insert_str(insert_index, rule);
insert_index += &rule.len();
}
}
// The current sequence will be used as the generator for the next round
}
sequence
}
}Note: The function above can also be written recursively but for larger iterations, you would run out of stack depth way before running out of heap memory.
For Barnsley Fern, the sequence expands as follows for subsequent iterations
| Iterations | Sequence |
|---|---|
| 1 | X |
| 2 | F-[[X]+X]+F[+FX]-X |
| 3 | FF-[[F-[[X]+X]+F[+FX]-X]+F-[[X]+X]+F[+FX]-X]+FF[+FFF-[[X]+X]+F[+FX]-X]-F-[[X]+X]+F[+FX]-X |
| 4 | FFFF-[[FF-[[F-[[X]+X]+F[+FX]-X]+F-[[X]+X]+F[+FX]-X]+FF[+FFF-[[X]+X]+F[+FX]-X]-F-[[X]+X]+F[+FX]-X]+FF-[[F-[[X]+X]+F[+FX]-X]+F-[[X]+X]+F[+FX]-X]+FF[+FFF-[[X]+X]+F[+FX]-X]-F-[[X]+X]+F[+FX]-X]+FFFF[+FFFFFF-[[F-[[X]+X]+F[+FX]-X]+F-[[X]+X]+F[+FX]-X]+FF[+FFF-[[X]+X]+F[+FX]-X]-F-[[X]+X]+F[+FX]-X]-FF-[[F-[[X]+X]+F[+FX]-X]+F-[[X]+X]+F[+FX]-X]+FF[+FFF-[[X]+X]+F[+FX]-X]-F-[[X]+X]+F[+FX]-X |
Step 2 - Draw the canvas based on the sequence
Now that the sequence is generated, we can start building the canvas. Each character in the sequence defines a particular set of operations on the canvas. This allows us to convert the sequence into a picture.
#![allow(unused)]
fn main() {
// Define length
// Set the angle to the LSystem angle
let angle_rad = -1.0 * PI * angle / 180.0;
let (mut x, mut y) = (0.0, 0.0);
let mut stack = vec![];
for seq in sequence.chars() {
// perform operations on the canvas
match seq {
// draw a line to (x,y) at given length and angle
'F' | 'A' | 'B' => {
x += length * angle.cos();
y += length * angle.sin();
context.line_to(x, y);
context.stroke();
}
'S' => {
// move along a line to (x,y) at given length and angle
x += length * angle.cos();
y += length * angle.sin();
context.move_to(x, y);
}
'+' => {
// rotate counterclockwise by angle_rad
angle += angle_rad;
}
'-' => {
// rotate clockwise by angle rad
angle -= angle_rad;
}
'[' => {
// push a point into stack
stack.push(Line { x, y, angle });
}
']' => {
// Pop a point from the stack and move to it.
let line = stack.pop().unwrap();
(x, y, angle) = (line.x, line.y, line.angle);
context.move_to(x, y);
}
// For others, skip and continue
_ => continue,
}
}
}| Iterations | Barnsley Fern |
|---|---|
| 1 | None |
| 2 |  |
| 3 |  |
| 4 |  |
| 5 |  |
| … | … |
| 8 |  |
Step 3 - Color the canvas using a linear gradient
The final step in generating our fractal is applying a linear gradient between two colors over our canvas. This can be achieved by applying color interpolation over each dark pixel.
#![allow(unused)]
fn main() {
let image_data = context
.get_image_data(0.0, 0.0, width as f64, height as f64)
.unwrap();
// data contains 4 u8 values per pixel indicating RGBA (red, green, blue, alpha) values
let mut data = image_data.data();
// Set the linear gradient colors : color1 -> color2
let c1 = Rgb::from_hex_str(&color1).unwrap();
let c2 = Rgb::from_hex_str(&color2).unwrap();
// linear gradient is defined using interpolation
// Assume the fraction grows from 0 to 1
// pixel.r = c1.r + (c2.r - c1.r) * fraction
// pixel.g = c1.g + (c2.g - c1.g) * fraction
// pixel.b = c1.b + (c2.b - c1.b) * fraction
for index in 0..(width * height * 4) as usize {
// Since the canvas is drawn with black, only alpha will be set initially
if data[index] > 0 {
// pixel's alpha is set
// Update the color using interpolation
let fraction = index as f32 / (height * width * 4) as f32;
data[index - 3] = (c1.get_red() + (c2.get_red() - c1.get_red()) * fraction) as u8;
data[index - 2] = (c1.get_green() + (c2.get_green() - c1.get_green()) * fraction) as u8;
data[index - 1] = (c1.get_blue() + (c2.get_blue() - c1.get_blue()) * fraction) as u8;
}
}
let slice_data = Clamped(&data.0[..]);
let image_data = web_sys::ImageData::new_with_u8_clamped_array_and_sh(
slice_data,
width as u32,
height as u32,
)
.unwrap();
// load the data back into the canvas
context.put_image_data(&image_data, 0.0, 0.0).unwrap();
}With this, a linear gradient between #C6EA8D and #FE90AF gives us

Note: Colors don’t exactly behave well with linear interpolation. For more details check out The Secrets of Colour Interpolation
Fractal Tree
Axiom : F
Rules :
- F -> FF-[-F+F+F]+[+F-F-F]
Angle : 22.5

Fractal Tree 2
Axiom : VZFFF
Rules :
- F -> F
- V -> [+++W][---W]YV
- W -> +X[-W]Z
- X -> -W[+X]Z
- Y -> YZ
- Z -> [-FFF][+FFF]F
Angle : 18

Dragon Curve
Axiom : FX
Rules :
- X -> X+YF+
- Y -> -FX-Y
Angle : 90

32 Segment Curve
Axiom : F+F+F+F
Rules :
- F -> -F+F-F-F+F+FF-F+F+FF+F-F-FF+FF-FF+F+F-FF-F-F+FF-F-F+F+F-F+
Angle : 90

Peano Gosper Curve
Axiom : A
Rules :
- A -> A-B--B+A++AA+B-
- B -> +A-BB--B-A++A+B
Angle : 60

Koch Snowflake
Axiom : F++F++F
Rules :
- F -> F-F++F-F
Angle : 60

Koch Snowflake 2
Axiom : F+F+F+F
Rules :
- F -> F-F+F+F-F
Angle : 60
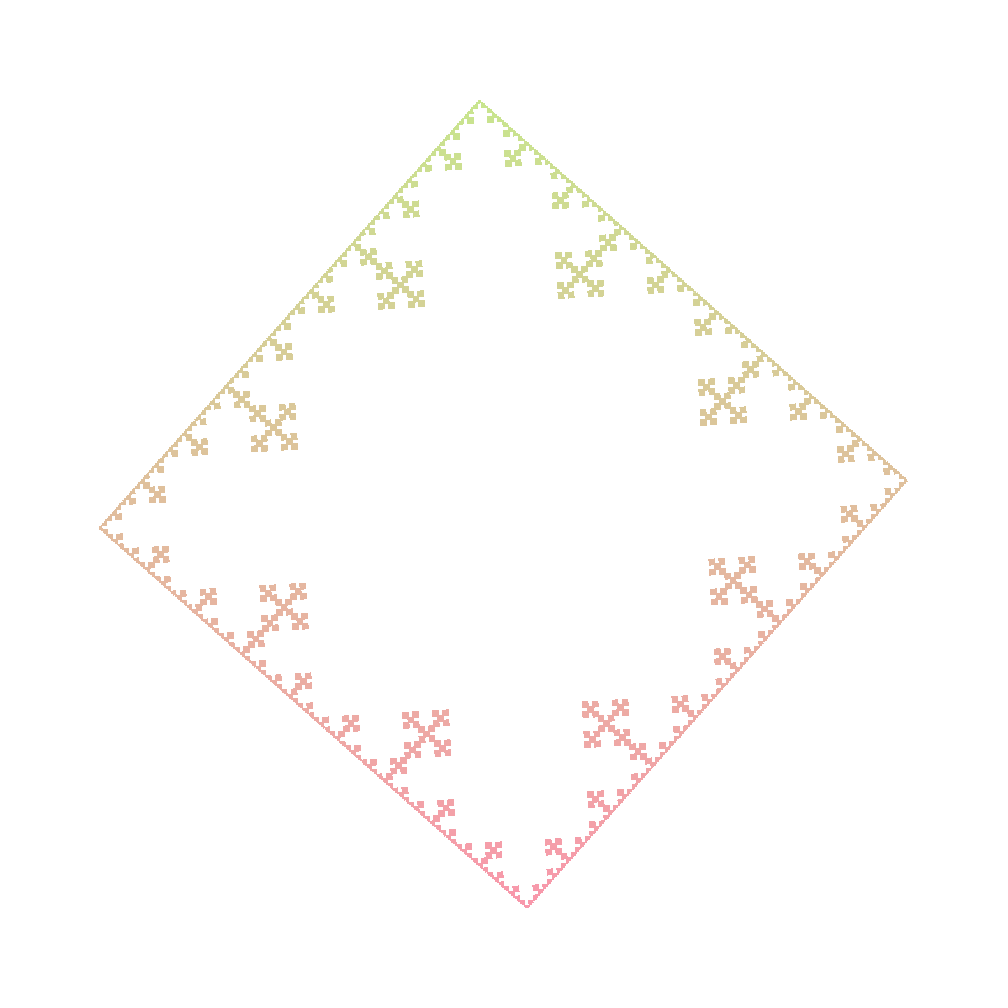
Koch Snowflake 3
Axiom : F
Rules :
- F -> F-F+F+F-F
Angle : 85

Quadratic Koch Island
Axiom : F+F+F+F
Rules :
- F -> F+F-F-FF+F+F-F
Angle : 90
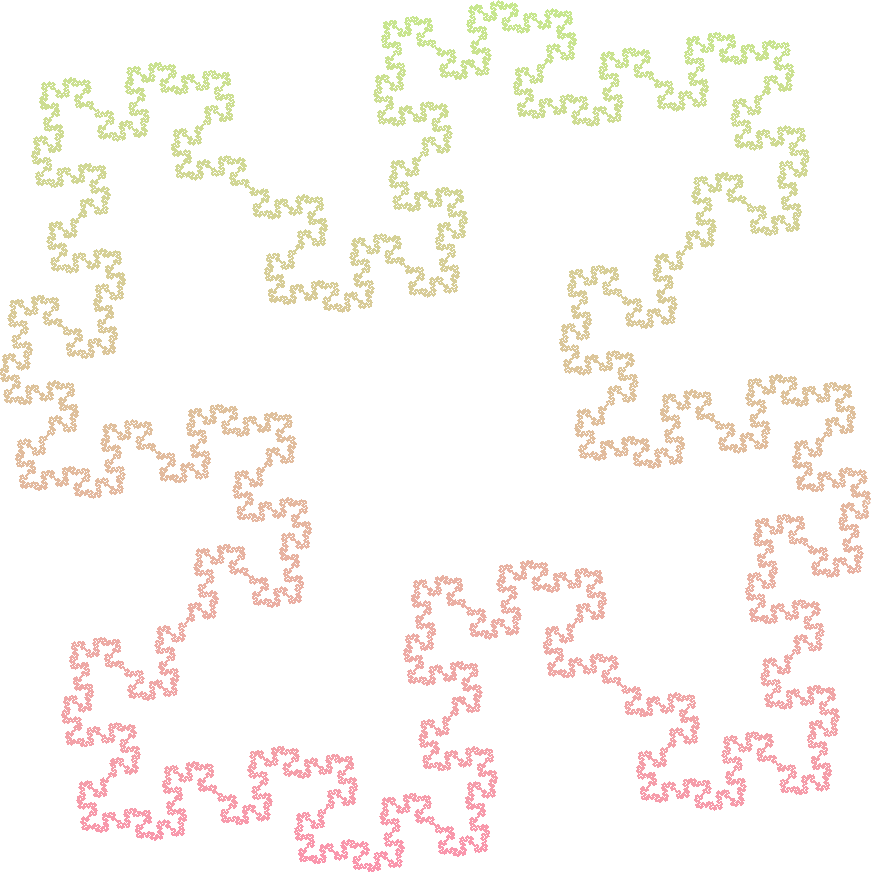
Quadratic Koch Island 2
Axiom : F+F+F+F
Rules :
- F -> F+FF-FF-F-F+F+FF-F-F+F+FF+FF-F
Angle : 90

Islands
Axiom : F+F+F+F
Rules :
- F -> F-SFF+F+FF+F-S-FFF-F+F+F-FFFF
- S -> SSSSSSSS
Angle : 90

Islands 2
Axiom : F+F+F+F
Rules :
- F -> F-SF+FF+F+FF-S-FF+SF-FF-F-FF+S+FFF
- S -> SSSSSS
Angle : 90

Sierpinski Triangle
Axiom : FXF--FF--FF
Rules :
- F -> FF
- X -> --FXF++FXF++FXF--
Angle : 60

Sierpinski Square
Axiom : F+F+F+F
Rules :
- F -> FF+F+F+F+FF
Angle : 90

Hilbert Curve
Axiom : X
Rules :
- X -> +YF-XFX-FY+
- Y -> -XF+YFY+FX-
Angle : 90
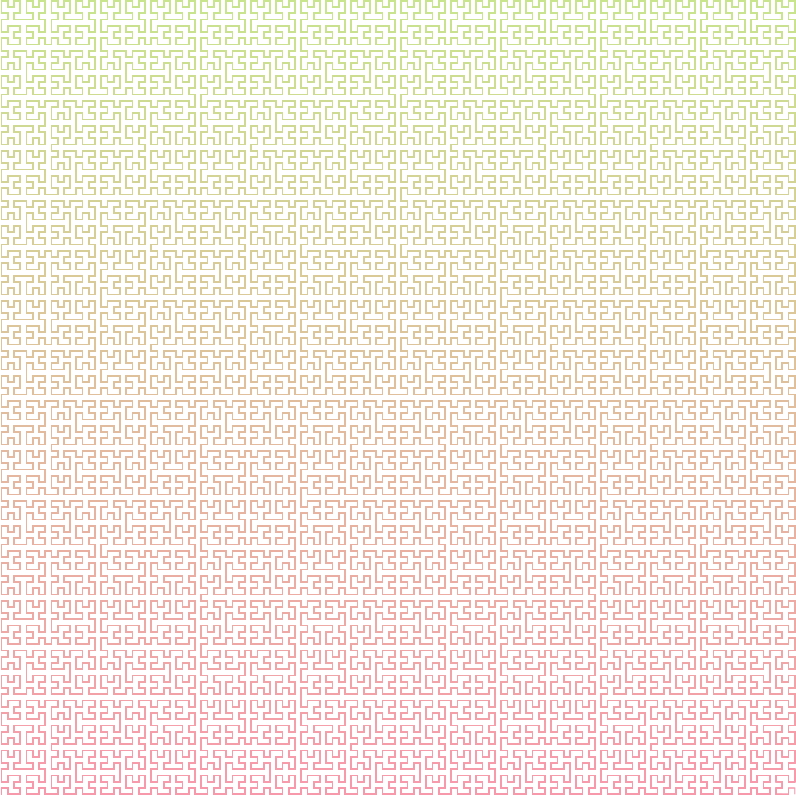
Frec Fractal
Axiom : XYXYXYX+XYXYXYX+XYXYXYX+XYXYXYX
Rules :
- F ->
- X -> FX+FX+FXFY-FY-
- Y -> +FX+FXFY-FY-FY
Angle : 90
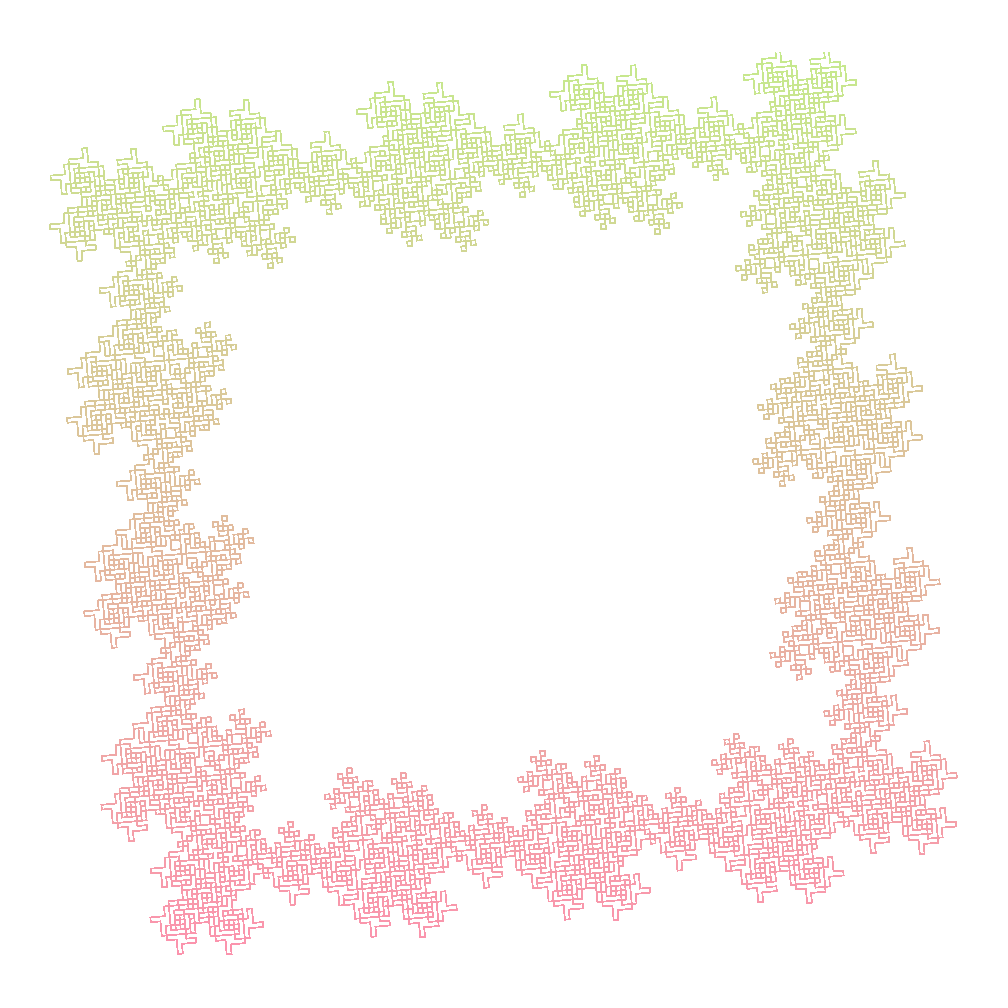
Archive
An archive of previous blog posts written in Medium
- Nov 05, 2019 Visualization
- Aug 31, 2018 Fractals
- Sep 19, 2016 The center of the Universe is not a black hole. It’s the opposite
- Aug 07, 2016 Choosing a good hash function
- Jun 25, 2016 How I downloaded Big Bang Theory Season 9 in my unstable network
Visualization
I have always been amused by how simple Mathematical rules govern complex fractals and designs. I believe the more we explore, the more closer we get to understand nature. I have listed a few structures I have explored over the years.
Kirby Krackle
Kirby Krackle (also known as Kirby Dots) is an artistic convention in superhero and science fiction comic books and similar illustrations, in which a field of black pseudo-fractal images is used to represent negative space around unspecified kinds of energy. It can be seen used throughout Spider Man - Into the Spider Verse movie to create the illusion of energy.
Audio Visualizer
A circular frequency visulaizer. I always wanted to try the media API and explore its efficiency on real time capturing. A Game of Thrones inspired page design. (Requires microphone permission)
Lindenmayer Systems
An L-system consists of an alphabet of symbols that can be used to make strings, a collection of production that expand each symbol into some larger string of symbols, an initial “axiom” string from which to begin construction, and a mechanism for translating the generated strings into geometric structures. Read more
Penrose Tiling
Penrose tiling is a non-periodic tessellation generated by an aperiodic set of tiles. A tessellation of a flat surface is the tiling of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. The aperiodicity of tiles implies that a shifted copy of a tiling will never match the original. Read more
Mandlebrot Set
It is a particular set of complex numbers which has a highly convoluted fractal boundary when plotted. Images of the Mandelbrot set exhibit an elaborate and infinitely complicated boundary that reveals progressively ever-finer recursive detail at increasing magnifications. The “style” of this repeating detail depends on the region of the set being examined. The set’s boundary also incorporates smaller versions of the main shape, so the fractal property of self-similarity applies to the entire set, and not just to its parts. Read more
Fractals
Fractals are infinitely complex patterns that gain shape from simple structures bound to various mathematical rules and constraints. They are useful in modelling structures (such as snowflakes) in which similar patterns recur at progressively smaller scales, and in describing partly random or chaotic phenomena such as crystal growth and galaxy formation. They act as to bridge to explain naturally occurring shapes over a set of fixed rules. Over this article, I have explored few of the fascinating fractals I have come across and the visual treat they offer.
Lindenmayer Systems
An L-system consists of an alphabet of symbols that can be used to make strings, a collection of production that expand each symbol into some larger string of symbols, an initial “axiom” string from which to begin construction, and a mechanism for translating the generated strings into geometric structures.
The L-Systems over controlled iterations provide us an unique string with perceived geometric properties. This motion is perceived using turtle graphics where the turtle moves with commands that are relative to its own position, such as “move forward 10 spaces” and “turn left 90 degrees” depending upon each variable in the string. The pen carried by the turtle can also be controlled, by enabling it, setting its colour, or setting its width.
Some of the constant literals of Lindenmayer Systems.
X → F+[[X]-X]-F[-FX]+X
-
F means “draw forward”
-
− means “turn left by some angle”
-
- means “turn right some angle”.
-
X and Y mostly does not correspond to any drawing action and is used to control the evolution of the curve.
-
The square bracket “[“ corresponds to saving the current values for position and angle, which are restored when the corresponding “]” is executed.
Fractal Plant
**variables** : X F
**constants** : + − [ ]
**start** : X
**rules** : (X → F+[[X]-X]-F[-FX]+X), (F → FF)
**angle** : 30°
Under 7 iterations, it produces this beautiful tree.

Dragon Fractal
**variables** : X Y
**constants** : F + −
**start** : FX
**rules** : (X → X+YF+), (Y → −FX−Y)
**angle** : 90°

Fractal Curve Tree
**constants** : F + −
**start** : F
**rules** : F → FF-[-F+F+F]+[+F-F-F]
**angle** : 22.5°

Closed Fractal
**variables** : X Y
**constants** : F + −
**start** : XYXYXYX+XYXYXYX+XYXYXYX+XYXYXYX
**rules** : (F → ), (X → FX+FX+FXFY-FY-) , (Y → +FX+FXFY-FY-FY)
**angle** : 90°

Code : https://github.com/Spockuto/LSystems
Live demo : http://vsekar.me/LSystems
Penrose Tiling
Penrose tiling is a non-periodic tessellation generated by an aperiodic set of tiles. A tessellation of a flat surface is the tiling of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. The aperiodicity of tiles implies that a shifted copy of a tiling will never match the original. It is self-similar, so the same patterns occur at larger and larger scales. Thus, the tiling can be obtained through “inflation” or “deflation” and every finite patch from the tiling occurs infinitely many times.
Penrose’s first tiling uses pentagons and three other shapes: a five-pointed “star” (a pentagram), a “boat” (roughly 3/5 of a star) and a “diamond” (a thin rhombus). Penrose’s second tiling uses quadrilaterals called the “kite” and “dart”, which may be combined to make a rhombus. Penrose Tiling Explained
This article explains the basic algorithm behind the tiling. Several properties and common features of the Penrose tilings involve the golden ratio φ = (1+√5)/2 (approximately 1.618).
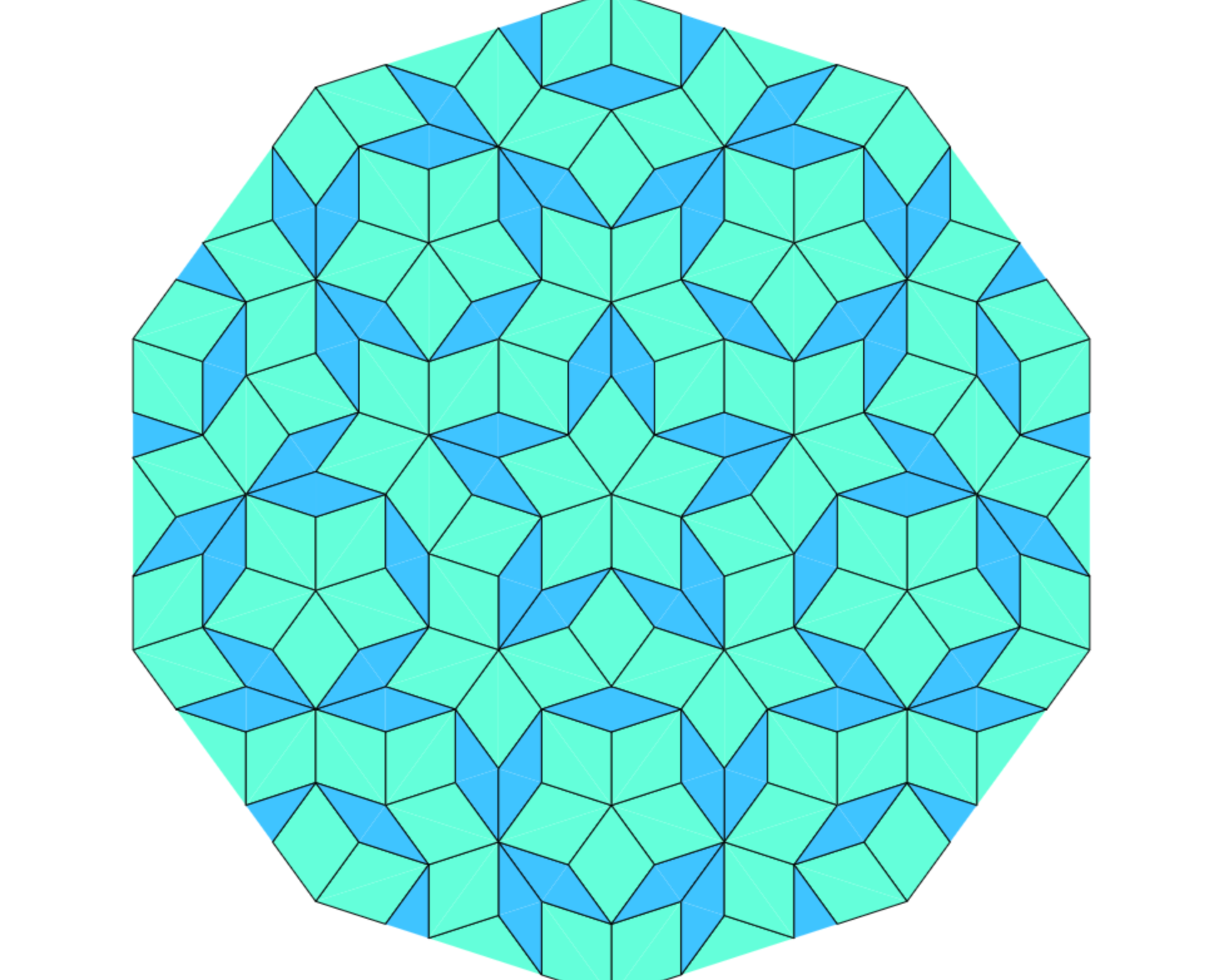

Code : https://github.com/Spockuto/Penrose
Live demo : http://vsekar.me/Penrose
Mandlebrot Sets
It’s the the set of all complex numbers z for which the sequence defined by the iteration :
*z(0) = z, z(n+1) = z(n)*z(n) + z, n=0,1,2, ... *
remains bounded. This means that there is a number ***B ***such that the absolute value of all iterates *z(n) *never gets larger than B. A bounded sequence may or not have a limit.
For example, if *z=0 *then z(n) = 0 for all n, so that the limit of the (1) is zero. On the other hand, if *z=i *( i being the imaginary unit), then the sequence oscillates between i and i-1, so remains bounded but it does not converge to a limit.
Treating the real and imaginary parts of *z *as image coordinates on the complex plane, pixels may then be coloured according to how soon the sequence crosses an arbitrarily chosen threshold, with a special colour (usually black) used for the values of *z *for which the sequence has not crossed the threshold after the predetermined number of iterations (this is necessary to clearly distinguish the Mandelbrot set image from the image of its complement).
**Images of the Mandelbrot set exhibit an elaborate and infinitely complicated boundary that reveals progressively ever-finer recursive detail at increasing magnifications. The “style” of this repeating detail depends on the region of the set being examined. The set’s boundary also incorporates smaller versions of the main shape, so the fractal property of self-similarity applies to the entire set, and not just to its parts.

Code : https://github.com/Spockuto/Mandelbrot
Live demo : https://vsekar.me/Mandelbrot/
The center of the Universe is not a black hole. Its the opposite.
Disclaimer : The theory is purely hypothetical and has no background to support it.

The wormhole is one of the most exciting phenomenon in modern day gravitational physics. The ability to travel millions of light years in mere seconds is a huge adrenaline rush for any normal human being. But this is the case for just one wormhole. Consider Infinite.
Background
The wormholes are an extension of Einstein’s General theory of Relativity relating the existence of gravity is due to the curvature created by the huge mass in the space time.

The curvature leads to all objects being attracted to a single source essentially giving rise to gravity. Every object with mass can curve space time. This single unified theory of gravitational physics has solved age old problems and has given rise to infinitesimal theories. One of them being Negative mass.
Negative mass
In theoretical physics, negative mass is a hypothetical concept of matter whose mass is of opposite sign to the mass of normal matter, e.g. −2 kg. The properties of this object would violate everything invented till now owing to the large criticism faced when it was proposed. However it was able to explain a large set of speculative theories including Wormholes.
Wormholes
If Einstein was right and every object with mass could curve space-time, then the object with negative mass could do the same too but in reverse.
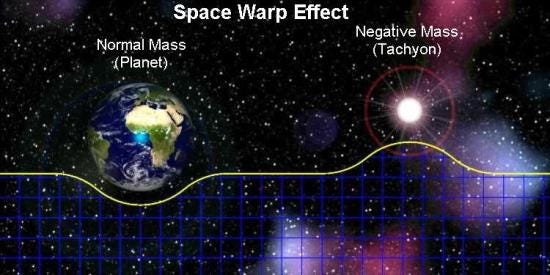
Consider a folded space time extending billions of light years. On one side there’s a huge mass curving space time normally. But on the other hand there’s a huge chunk of negative mass curving the space in the opposite direction. Since they are curved in opposite direction and space is folded, they are due to meet at a single point achieving a tunnel between the two space-time.

This tunnel is a link between two space-time separated by billions of light years but now at the distance of few feet. This theory has been widely used in many movies making it more fictional. The complicated math existing behind them proves that achieving such a stable wormhole is impossible provided with the present day technology.
Spherical Wormholes
Coming to my theory, wormholes can be simplified as a pipe with two ends. Also the length of the pipe can be controlled by the amount of mass present at both ends.
Consider a hypothetical space, where each pipe is of equal length and they have a fixed center. It is basically a sphere of space-time so curved and convoluted, it gave rise to infinite wormholes which are the diameters of the sphere. They have a positive mass curving space at one end and a huge negative mass at the center curving the space in opposite direction.
This gives rise to a structure similar to that of an atom. This protons are the condensed huge negative mass and electrons are the infinite celestial bodies curving the space-time on the surface of sphere. This gives rise to an medium for not only to travel between two space-times, but infinite. This also provides an understanding to the structure of the universe (Maybe?)
Such an huge amount of negative mass is condensed at the center of the universe. This might give rise to what we can call a
Super massive Anti black hole (SMABH)
It is not a white hole /\
A single entity with huge amount of anti gravity, which basically does everything opposite to a black hole. It repels everything in existence, including space-time. If space-time is a sphere and a SMABH exists at the center, It could repel everything away explaining why the universe is expanding. It could also explain why the relative distance between two objects increases as the surface area of the space time expands.
But how does it still expand?
The answer lies within Hawking’s equation. It was proposed that a black-hole continuously looses mass and achieves singularity. Proposing a reverse theory would imply the increase in the negative mass of the SMABH causing more repulsion. This is why the universe is still expanding.
But why aren’t the wormholes exploitable?
The curvature in space-time caused by this entity is high but since the space is expanding away, they never meet contradicting the theory of infinite wormholes. However, huge masses like super massive black holes are able to exert such curvature, such that they finally meet. This opens a wormhole inside the black hole where the tunnel basically redirects us to the center of the universe. However objects are short-lived there because of the high intensity of radiation. This is the reason why wormholes have been not been able to be exploited till now.
Why does the universe appears flat?
This is similar to the phenomenon on earth. Are we able to explore the curvature of the earth? No because it has a very high curvature making our line of sight flat. The similar applies for the universe. Maybe we need to invent new technology that could explore the farthest of the universe which could provide a slight hint of spherical space-time.
This is just one of my personal theories which may or may not be possible. Also, this could affect the nature of everything found until now. But according to the Law of Infinite Probabilities, this might be true one day. I really hope it does.

Choosing a good hash function
Securing your application is one of the hardest part of the development cycle. There are a lot of security aspects one has to look far ahead and variety of tools are available to solve each issue. But choosing the right tool is always a hardship. Specifically when it comes to encryption or hashing.
Passwords
Hashing passwords is the best way of storing passwords in database. But it is’t that simple. If your database is compromised and you have just hashed the password, they could easily look for matching hashes by constructing a Rainbow table with commonly used passwords.
Salt
To solve this problem, every password is concatenated with a random string called the SALT and then the string is hashed. The salt is stored in the database and used when we have to authenticate the user. This increases the security exponentially as there won’t be any common hashes and finding a correlation between the salt and hash is practically impossible.
However choosing the right hash algorithm is difficult. People always use the obvious choice SHA1/2/3 which is completely wrong. SHA is constructed mainly to be fast making them suitable for large files. They have a speed of 12–15 cpb and hence bruteforce is highly possible. A more preferable algorithm for hashing is pbkdf2-hmac which repeatedly uses SHA on the logic of a PRNG. These algorithms are relatively slower that SHA and hence takes bruteforce out of the table.
Files
The SHA algorithm is specifically designed for acting as a digital signature to large files. The SHA1/2/3 algorithms are designed by group of cryptologists who compete in the competition organized by NIST. These competitions are conducted when a collision is detected in the previous SHA. Before SHA, Message Digest was “THE” secure algorithm. Nowadays people barely use it because of too many collisions.
Every software is provided with a hash which helps us to verify the authenticity of the file. However this can only help us identify if the file was damaged during the download. If someone was able to hack into the website and modify the software, it’s doesn’t take much time to modify the hash too. Hence there isn’t a completely secure way to check the authenticity of the file.
The main factor which comes with hashing large files is speed. SHA2 provides a speed of 208mbps. However this can be further improved. A tree based hash structure is constructed which improves security as well as speed by utilizing the multi-core system. Merkel tree is widely used nowadays. The present SHA3 provides us with Sakura method for a tree based hash construction. These are much faster than previous algorithm and hence large files can be hashed easily.
Data encryption
The data encryption is used to encrypt files when transferred over unsecure networks so that even if the file is retrieved they couldn’t be accessed. The algorithms use for this purpose are DES and AES which work on a key based encryption. However software gaints develop their own encryption algorithm which provides even more security as the algorithm isnt exposed. One such example is how YouTube URL is produced from just the Video’s title (or maybe more :P)
Key Exchange
There are times when we need to transfer to a short information but must be highly secure. This is established by RSA. RSA was one of the primitive algorithms which uses key based encryption to transfer data. Key based algorithm are of two types
-
Symmetrical (public)
-
Asymmetrical(public/private)
DES and AES are of symmetrical types. RSA is an asymmetric algorithm. It uses public key to encrypt which can be decrypted only by the private key. These algorithms are slow and hence used only on very short information.
Modern day money is Bitcoin. They use a further complicated algorithm called ECDSA which is widely used nowadays.
This is just an outline of where hashes and encryption are used frequently. Some algorithms like Blowfish, bcrypt, BLAKE2 haven’t been mentioned here but at specific constraints, others don’t stand a chance against these methods.
May the security be with you.
-
SHA — Secure Hash Algorithm
-
CPB — cycles per byte.
-
PBKDF2-HMAC — Password-Based Key Derivation Function — Hash Message Authentication Code
-
PRNG — Pseudo Random Number Generator
-
NIST — National Institute of standards and technology
-
DES — Data Encryption Standard
-
AES — Advanced Encryption Standard
-
RSA — Rivest,Shamir,Adleman
-
ECDSA — Elliptic Curve Digital Signature Algorithm
Useful Links.
-
https://www.addedbytes.com/blog/why-you-should-always-salt-your-hashes/
-
https://en.wikipedia.org/wiki/Advanced_Encryption_Standard?wprov=sfla1
-
https://en.bitcoin.it/wiki/Elliptic_Curve_Digital_Signature_Algorithm

How I downloaded Big Bang Theory Season 9 in my unstable network.
I take serious measures to get things right when it comes to downloading TV series. But today, I have been proven wrong. My day goes like this.
I planned to download Big Bang Theory Season 9 after another exhausting FRIENDS marathon AGAIN. I followed the routine.
Put the torrent magnet on direct-torrents and wait for it to be seeded.
I even clicked the → button and believed it would actually fasten it. But It almost took three hours to be seeded and the file to be available.
I have a 512kbps extremely unstable internet connection. It would take a day to download 3GB. I hate downloading files via Chrome because you can never resume a download there. So I use wget and there comes my 2nd problem. The files were served via SSL and so wget kept throwing me 403:FORBIDDEN. I tried the download on Chrome and it was working fine. So I made my wget fake the connection that the request was actually from the browser by changing the User-Agent. With a simple wget -U “Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/50.0.2661.94 Safari/537.36” the download starts working.
ETA 22 hours.
As I expected, It was going to take a whole day to complete the download. It was midnight and I had to find something to keep me occupied for one whole day which doesn’t involve my laptop. Right then, I got a text message.
“Buy 2 Get 3 free”.
Problem Solved. But the bus trip was gonna be boring. So I thought maybe I can download a movie which I could watch on the trip. I deleted Big Bang Theory from the queue in a way that doesn’t affect my download and added FINDING DORY ❤ to the queue. Since the torrent had a high number of seeders, It was instantly available.
ETA 10 hours.
I had to leave the by 6am. So I stopped Big Bang Theory download. But direct-torrents doesn’t have a user cache. So I had to seed Big Bang Theory all over again because I deleted it from the queue. I added it to the queue and the movie was downloading without any trouble. Time for a pleasant sleep.
ETA 4 hours. The next day.
I woke up and found FINDING DORY downloaded and Big Bang Theory was ready to be downloaded again. But I had already downloaded some part of that zip file. Thanks to wget -c,it was back on track resuming from the part where I stopped the download. I was going to leave my laptop unattended for a whole day and so I prepared it for the worst. I gave it the lowest display power and lock screen on 5 seconds of inactivity. I could have just closed the lid and went with no suspend but somehow it interfered with my Wi-Fi connection. My laptop can run for 3 hours without power in this setting and that’s better than most.

ETA 18 hours.
I returned home by midnight. I get into my room to check the download. It was at 98% but has become static. This means direct-torrents removed the file as I couldn’t complete the download in a day. So I add the file again and waited for another 3 hours.
ETA 20 minutes.
It was wget time. The download ran for some time and again stopped because of network reset. I use wget -c to get it back and I know the file is still available because if not I would have got a 404. The terminal said.
The file is already fully retrieved; nothing to do.
But I’m aware the download stopped at 99%. This means I have a broken zip which I am unable to resume.
ETA 10 minutes.
So I thought maybe I could extract the zip file and just download the files that are damaged. Extraction succeeded. Yay!!
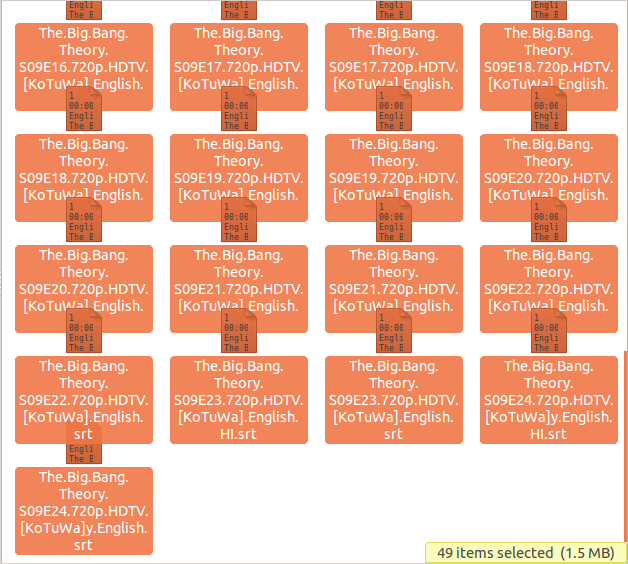
The folder contained 48 SRT files alone.

The zip file was clearly 3.6GB but the extraction only had 44 SRT files which were merely 1.5MB. Back to square 1.
ETA -_- I still didn’t lose hope.
I opened the file in Bless and checked for .mp4 hex. Results found : 72.

So Yes, All the episodes were in there but I couldn’t extract them.
I tried to fix the zip file with zip -FF but it just returned me an empty zip file.
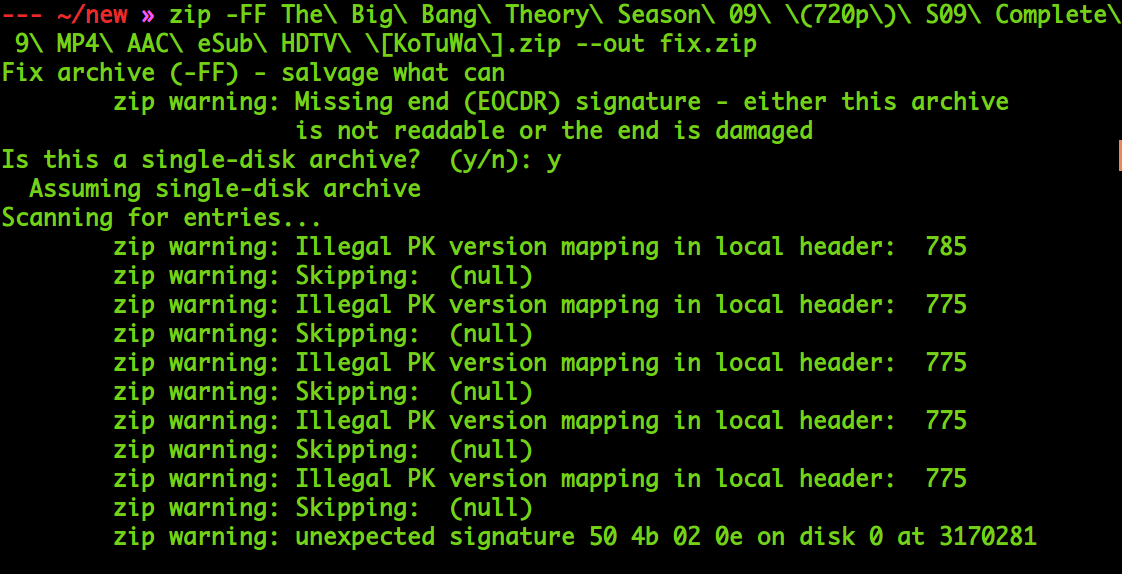

The file wasn’t broken but something has gone wrong. I go back to the torrent site to check the file structure. The zip file consisted of all episodes in mp4 and a compressed file of all subtitles.

Out of options, I tried unzipping the file from the command line with unzip.
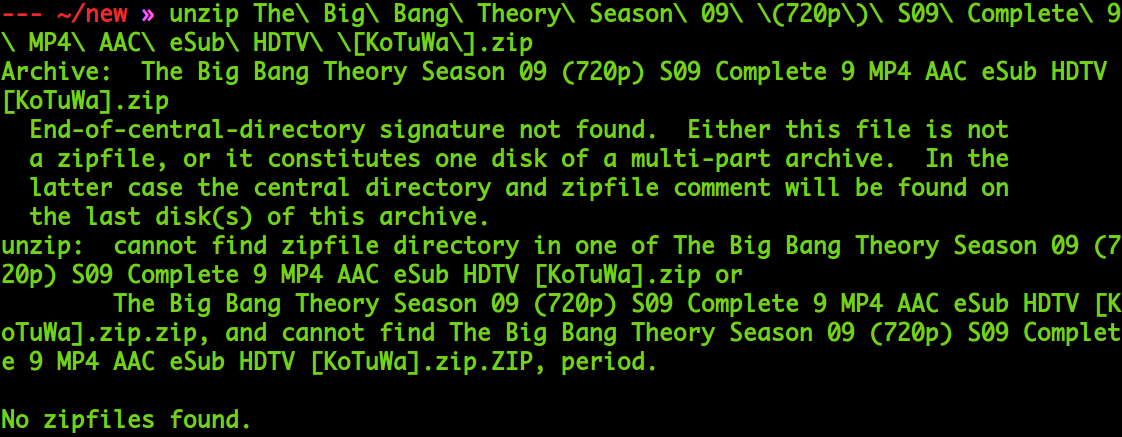
It threw an error “End-of-central-directory signature not found”.
The problem was clear now. The file download wasn’t completed. When the network reset occurred, the compressed file with subtitles was downloaded. When I tried to resume to download there was an EOF mismatch with both compressed files which made wget think it had fully retrieved the file.That is why on extraction in GUI, I got the 48 srt files and the zip -FF couldn’t fix the zip.

ETA 0 minutes.
Time to Google. I checked for file extractors which doesn’t check for EOF. After an extensive search and skimming through stack-overflow, I found that jar files were actually inner zip files but don’t have a End-of-central-directory signature.
I took a leap of faith and tried to extract zip files as how we would extract a jar file using jar -xvf.
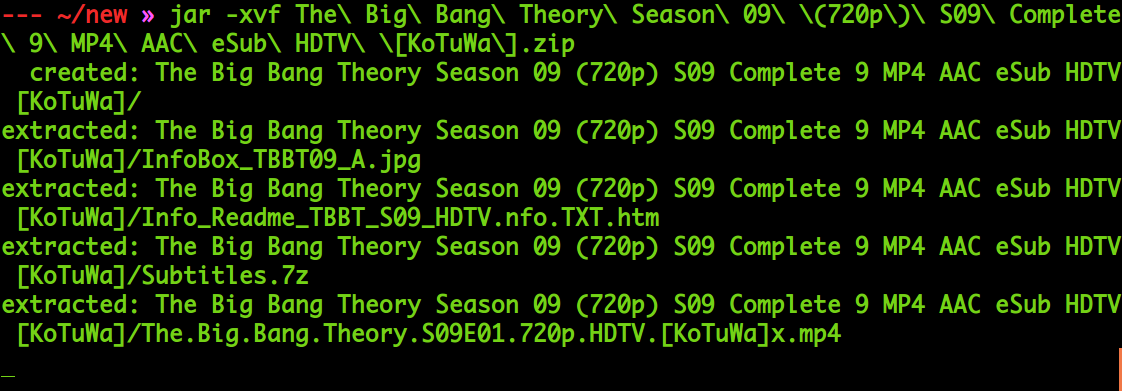
The mp4 files were extracted one by one and the corrupted file was just the sample mp4. At 4am, I finally downloaded Big Bang Theory season 9 completely.

To be honest, the season sucked BIG TIME.

Markdown Template
- Heading
- Emphasis
- Blockquotes
- Lists
- Latex
- Codes
- Tables
- Links
- Images
- Footnotes
- Task lists
- Blog Specific
Heading
# h1 Heading
## h2 Heading
### h3 Heading
#### h4 Heading
##### h5 Heading
###### h6 Heading
h1 Heading
h2 Heading
h3 Heading
h4 Heading
h5 Heading
h6 Heading
Emphasis
**This is bold text**
__This is bold text__
*This is italic text*
_This is italic text_
~~Strikethrough~~
This is bold text
This is bold text
This is italic text
This is italic text
Strikethrough
Horizontal Rules
___
---
***
Blockquotes
> Blockquotes can also be nested...
>> ...by using additional greater-than signs right next to each other...
> > > ...or with spaces between arrows.
Blockquotes can also be nested…
…by using additional greater-than signs right next to each other…
…or with spaces between arrows.
Lists
Unordered
+ Create a list by starting a line with `+`, `-`, or `*`
+ Sub-lists are made by indenting 2 spaces:
- Marker character change forces new list start:
* Ac tristique libero volutpat at
+ Facilisis in pretium nisl aliquet
- Nulla volutpat aliquam velit
+ Very easy!
Ordered
1. Lorem ipsum dolor sit amet
2. Consectetur adipiscing elit
3. Integer molestie lorem at massa
1. You can use sequential numbers...
1. ...or keep all the numbers as `1.`
Start numbering with offset:
57. foo
1. bar
Unordered
- Create a list by starting a line with
+,-, or* - Sub-lists are made by indenting 2 spaces:
- Marker character change forces new list start:
- Ac tristique libero volutpat at
- Facilisis in pretium nisl aliquet
- Nulla volutpat aliquam velit
- Marker character change forces new list start:
- Very easy!
Ordered
-
Lorem ipsum dolor sit amet
-
Consectetur adipiscing elit
-
Integer molestie lorem at massa
-
You can use sequential numbers…
-
…or keep all the numbers as
1.
Start numbering with offset:
- foo
- bar
Latex
* Inline equations are replaced with `\\(` *text* `\\)`
```
\\( \mathbb{N} = \{ a \in \mathbb{Z} : a > 0 \} \\)
```
\\(\mathbb{N} = \{ a \in \mathbb{Z} : a > 0 \}\\)
* Block equations are replaced with `\\[` *text* `\\]`
```
\\[ \mathbb{N} = \{ a \in \mathbb{Z} : a > 0 \} \\]
```
\\[\mathbb{N} = \{ a \in \mathbb{Z} : a > 0 \}\\]
- Inline equations are replaced with
\\(text\\)
\\( \mathbb{N} = \{ a \in \mathbb{Z} : a > 0 \} \\)
\(\mathbb{N} = { a \in \mathbb{Z} : a > 0 }\)
- Block equations are replaced with
\\[text\\]
\\[ \mathbb{N} = \{ a \in \mathbb{Z} : a > 0 \} \\]
\[\mathbb{N} = { a \in \mathbb{Z} : a > 0 }\]
Codes
Inline ` code `
Indented code
// Some comments
line 1 of code
line 2 of code
line 3 of code
Block code "fences"
```
Sample text here...
```
Syntax highlighting
``` js
var foo = function (bar) {
return bar++;
};
console.log(foo(5));
```
[Rust specific mdbook configuration](https://rust-lang.github.io/mdBook/format/mdbook.html)
Inline code
Indented code
// Some comments
line 1 of code
line 2 of code
line 3 of code
Block code “fences”
Sample text here...
Syntax highlighting
var foo = function (bar) {
return bar++;
};
console.log(foo(5));
Rust specific mdbook configuration
Tables
| Option | Description |
| ------ | ----------- |
| data | path to data files to supply the data that will be passed into templates. |
| engine | engine to be used for processing templates. Handlebars is the default. |
| ext | extension to be used for dest files. |
Right aligned columns
| Option | Description |
| ------:| -----------:|
| data | path to data files to supply the data that will be passed into templates. |
| engine | engine to be used for processing templates. Handlebars is the default. |
| ext | extension to be used for dest files. |
| Option | Description |
|---|---|
| data | path to data files to supply the data that will be passed into templates. |
| engine | engine to be used for processing templates. Handlebars is the default. |
| ext | extension to be used for dest files. |
Right aligned columns
| Option | Description |
|---|---|
| data | path to data files to supply the data that will be passed into templates. |
| engine | engine to be used for processing templates. Handlebars is the default. |
| ext | extension to be used for dest files. |
Links
[link text](http://dev.nodeca.com)
[link with title](http://nodeca.github.io/pica/demo/ "title text!")
Autoconverted link https://github.com/nodeca/pica (enable linkify to see)
Autoconverted link https://github.com/nodeca/pica (enable linkify to see)
Images


Footnotes
Footnote 1 link[^first].
Footnote 2 link[^second].
Inline footnote^[Text of inline footnote] definition.
Duplicated footnote reference[^second].
[^first]: Footnote **can have markup**
and multiple paragraphs.
[^second]: Footnote text.
Footnote 1 link1.
Footnote 2 link2.
Inline footnote^[Text of inline footnote] definition.
Duplicated footnote reference2.
Task Lists
Task lists can be used as a checklist of items that have been completed.
Example:
```
- [x] Complete task
- [ ] Incomplete task
```
This will render as:
> - [x] Complete task
> - [ ] Incomplete task
Task lists can be used as a checklist of items that have been completed. Example:
- [x] Complete task
- [ ] Incomplete task
This will render as:
- Complete task
- Incomplete task
Blog Specific
Things to figure out
- How to add date / time for the blog. Shortcut for adding current time
- Adding the coffee place and template
Public Keys
SSH Pub RSA
ssh-rsa AAAAB3NzaC1yc2EAAAADAQABAAACAQChqdy+sOVrlucDhDljC+t+5FPgSqC9PgFJiDmFOGxPCBej5ADaqnoMgPxXLIaU7DxGQ3Go1unkYAJnypFyHIzQHL04uELjkOYJEB0qAfpYj0EZiSVHI2grPu+3F8v4gt/U/K0l8xz2tvIY13N2b5VhAso53GzfICkF+5pauf7YBRVX/nrs7LJxV/bUmjQOGbmrIxZDwJet070mSuRU3ajMFaahwmTsBotF2d+fL8xpIJnEOikwPu8OZnN4ClUJIThZ/17FxRfEmbeSg6NyGKabCigRi1/EwoscTlhlp1EOaTGjo2vwE9/DvJNEhQWAr2QtbIRqzMj0TIiEc12bqK3bYFxQC/gbceo9B+s6eT9dj1PQedKFUmj78LTrUoINE1vhxuM00EwBYocc4tLqQroLS/VfZvPddMQ0wFrB5/fY54Ji51SVpqneEXWC0cwrXtjdnC9XJm1ArsTbcAgCTh5kOJmK6+8AZRgFm09Cgd6YxAO0p1r90rsFVp5rcUgHtGDHz1EoP8RVycs2COxoYdZYVC7LOfnxdcovrvTSDrFRvQmr9VkcdA4BaJB53A7fEUw7SG6cqVy6Pd4EdvIXek91gA83HEjSnK+TgoRYiblL9Lq8ZHXjNwNK7PqXTaESIOjzuZN/ECut0HDZmMFVZKeiF3G31r/cb+JKf4g1ta6uxQ== [email protected]
SSH Pub ED25519
ssh-ed25519 AAAAC3NzaC1lZDI1NTE5AAAAIHS16h0N5RIhEGV3xtFYvbxrh09K4sm2aLocGDD51oBM [email protected]
GPG Pub (Personal)
-----BEGIN PGP PUBLIC KEY BLOCK-----
mQINBF3BfcwBEADMwzJ6+q5sY4THccmPKAYC0B50FaT+BbclOnyhabvaJZjq+l0P
lNsss5O67BlLGR9B2VAq7OhxvJuq39heIC6E82Ax6HARbp4c3kDzemKFMW5RfIwJ
qEvRCBsvrxCpbl09B5DA3uWsceLcWJKdTH5Rql4MlGyReWhWqsZDW9rr4uumHAvL
LdT+xo8wb6tYllJyv1Zn5WehkxwyjpIu363c7W0jqS+mvLk8zk4lne19NZMQc9rD
hOhxke0hdOr3MU9K2s4M6OyqsiohZhQ+0o4MK+vKNYESMOiMR9lEH1cuqnXmErfN
P67rU3v+1Bpd8Az0eonKepKr1DMBWWzObjgTbI3EpAFu8CShxFqmqpmBFULqDWQC
ZphYxg1lJRwvDNlkqvTLCS8cL6bftSuz4QjYP2gE1Bm9zQCjIShp9wcbPdkD3IKz
sb331YBx+vgXKeaMnwCRRpniUUYJNWWScXzURp4LpchrKtixxRczoYFQRTPvQM5Y
aUDXOTTULPhadZ8SfOy8Ue0zHMIIITwwrcHjTzV9yY0FFg1Vs6yOrOZ7ejnAw9tZ
qbEi9zEn5VPxQJwfmyQ35pMGtI5TIHDRyH2KhONNgpBoAKnwrczJIu0QlomQJwVf
L5rAhwYT+R1Z4ZNsdqzZ2Iy3Ak1zIGaMKhS6SR1wPB9IGAH6vIIEXBfKzwARAQAB
tDtWZW5ra2F0ZXNoIFNla2FyIChQZXJzb25hbCkgPHZlbmt5dGhlc3VwZXJzYWl5
YW5AZ21haWwuY29tPokCTgQTAQoAOBYhBMjLaS4Bq8fluWeohzRKk5SFMHX8BQJd
wX3MAhsDBQsJCAcCBhUKCQgLAgQWAgMBAh4BAheAAAoJEDRKk5SFMHX81r8P+wRu
2wJgUdjZeCmW1WRiHU27INPllpjcPGZVnyIbqRCtGPHn5BSyYPOwrDOt0AcfRbSo
1oq0XeaO9i6+t1dNAIXv6pjNS2va0unYpWWKb5URxFyEI0fk0jmNbWL7Xiloq5V4
YoY2n4kKSNwFPfT35QOrpuiA+o+XuFWYDPsb0IUJLJpxcOltH5dbcjI/cR3/fnBT
MoKG340M+V53maCkksOl32HQMge2ezIQzwdXpPx52T9gCTywmCpS76xYzjmjkHUa
1mGmSG5XlYGxtAqKxPm/Nmge8yW7Fv1sFFAAqvhqJ1dX8QUCDItwrVueszJ8rjdJ
xQiQE/PGkD562c46wN/3LMghqV2DhMAfFjZdr6lZbkqt83Pm1GE760kE9XS9mZW2
8wys9pcmRNf39jP6lRUBLycarRMEYHAG89VbBwfQk2GjUPNdYewZMfYhvrchJ7pA
sZkXvZjVwzecSuxpQSkYLmkA9dJ6N29yASuEXnTGtBaWlgGTawiYodR0T6K/oco+
9PqGa/AFTrbY58yo3geSu182chPhQX9qpSB76E3cX5PGPFn5f3EZGBaDhgccDSBK
t4Ll/bHw+vMAfeQKqe7yrv7rfsh9hIXue5L7y8bD7YW1u+j4IJWwWT31kiMmWfze
5SmLSQjjiAJSioVAEZhPyYVgLrTdFHumM+Rv6ri5uQINBF3BfcwBEAC3xytlAyTK
I/Rf8p+Ne9rNZUxnP4Srt47JOgrq6CnXKQb3fro16axGySXwAroUGmSXRdOO+E6d
NsaiNiurI+6IZEMAz1jYykoUzVI7OEworT+bOmawaVasOPypkHRCCntI367t7BIM
sZ20+apqhvVCMhoWVkrRXwZpODKw49obUeQsFBbvMG3vZwKOw3TxrsdjQ48zn8pB
CXU3QNih340fqK7/2tU7Ojg2+Xka4vfciMt8zYK1DiiPPxv/lRiI1x5XLokn7oBL
6SJw+5iUI4bwGqp3T0lpMx4AmAlgSMJGqI68wA4wFeqWpPi8N+0LYaGCl3fg2C8f
zUpFBLQMREu+JSo+N6XEmhuAGjMC3k1HSPbBhYefhITxTq+tFmofMhLATaUsyLhS
e5JRI8Pbgam5H5b/N4nL97KSnTDjaqgEQZm1Cyn6iAMvvxhYriCFFxOWNSjEMfJK
UoyS8OtKlrYq+zdnJ89Bqu3zvvcoxK8Hy013TCAgDPUgdUNTZUH/48rKtE3Ts7N6
FGqUgL4CD0ii3KchEo0w5jQfvrrzImy0JO6ITzmXK98d9tGKHKwrxGjGMjk5xDsM
PBkMw2msNSKd4IZ/T9UyzBshcikeLJlykX3iirX1kg/e6TqLYFT8H8FZnnVssSUJ
tcIlu5K+2Fi0r3fqKm4xU3wacIJ7QLZ3/QARAQABiQI2BBgBCgAgFiEEyMtpLgGr
x+W5Z6iHNEqTlIUwdfwFAl3BfcwCGwwACgkQNEqTlIUwdfx0jA//ZMAxsPyjHVur
Pwgm2i42Qc3OBPfsSUMBJbaSG7tzF6l9h1V/zQwBJpe2Ita1NR2CViToOPTgKND2
Ui0vtiughhx99wscBnMGE75ceLjhLYagoIsmNp+uFeSIls9gZN9/NyoowpW14t82
a6ib82ELYxxk7dVO5s80TKkZjj+AL5HlIrdLECuewSMyxyT5lq1QSQKDI60umByR
MRz2yRbuk9nbpKTidq3+ZAssSa2Za9wjJe8C4Q+rPv2B4MSDTeq7P6ORrkqZhFx0
J+7ZnlaAUnTPEuVS/r0YVh3XGjz1V7Bpm6slLcnE7thO+n10wj7+DrLpZFTYRr3J
rHcsQ4cyGoQ3adzvq6Pax6DWjf+CbcR84qrwkMbj9Zkn0YKwjwKdZZ7VPWHfFlKB
pLljN3mO+/jt5lT0HFNg9mbT5SF/06/SSXOGRSoJUsc+hsmNuVEcoT2IZ6WQsqcX
8Me8xSP1T+qTUTIhATrf2ckl5/SqDMYtMbAbn3BXhFCxS92aNf7NZnkej4zJnIz/
PmaIw7SnhrGCmIO4bbl22aiZWHGuMG+ST2L4rUjudmrSHjjQVyFHxzBpCDGW3iQv
liU2uWfKP55XzHzunhUE8+/O28Wecdu84UsrQJj6ssD7IDxWOKYNRop24YFsNFlR
uLwaa+tYHEAIwB7iDD3T9chiWgUAsdE=
=VDIH
-----END PGP PUBLIC KEY BLOCK-----
GPG Pub (Official)
-----BEGIN PGP PUBLIC KEY BLOCK-----
mQINBF3BfpwBEAC0Vt20c5AXsbIVldwevBCSub5IsJkIyQyVqHsGlrRy2lvye7bc
GrQn8BIDCjcCRgTXatTMuXQ9L/lb+/jXDKApGatdC86I4cotXa8NvjAuBQrkdbzJ
veFGJMvi+MNPcWBhn+e28MU0g6c8cvFL4U/fNP+dTMqU8S4HWq8pw3YU0AKi/amm
8RMGjx9ZBxquY1STcww0/NTZvzeUcEROwtcmlohZgrMfc27VON49l5v8A4kG0dP7
8hVwvzMkK9NhwTPdXvaxYKMB6dIYS7VuYZogWRlUuzK8ayiZ/x9ckfjn40RMtbzo
3vyeKImhEK1FAjk4s2ldwb9bWMkf8/9kj9mT9356wUC6Y3sT2X9EgVDBVFr9cWZT
XfC52tlW3iJjygt7tlkD1ZftnNhAzPz79qpGn+YU0qetoz0+klp8rSf2wqFy0kIT
+SDKK2Pvd0QMo41RDTVmorJQvUca7eDJWiwmJeCkjgMN5zHex3JQIc5KLwgQB/pz
y4HgvDBlXLSwfPyc1DquEGD31m4dMogE+5vSJqVmUEF2DfT4C9zlhgSg3QMGBCTp
XaHevwzbRDkf4xtdtfluONnbEj9hpmNIvXY6xv/0ZVHMfeqJE6NytcyUTeuSkX/B
5iuymnBn61NC6S1iFV9gsDihyvx2HFm+Hm6AsYg1Wy1CWoRo2TWmJfMLOQARAQAB
tDhWZW5ra2F0ZXNoIFNla2FyIChPZmZpY2lhbCkgPHZlbmtrYXRlc2guc2VrYXJA
Z21haWwuY29tPokCTgQTAQoAOBYhBNLqj2fG2knmZPSc2tUrTRlQqDHABQJdwX6c
AhsDBQsJCAcCBhUKCQgLAgQWAgMBAh4BAheAAAoJENUrTRlQqDHAGRIQAKLH8+rL
Lm03C6unpbwvK3va7uzn010mbGbfHLJFUQUMwxmVkudWRVdaT1FYyEOo56atMusv
lMGqXo4GK1rPn7Yl2909gnQgMIpVI0sgUfe9pnnQ3He7O5pemQhWjo+dXHyfVxc+
M+23BBv30Rrfj8wR0IFixyguMPNvannAbrgpU+z31p0VPtfRVr972uOlCvY9SZqa
uukoQyzegnaWQYzvfr1pzi4cN/E8YgTLTSBs4kwvVrauhKVX/b2Ypw7ltatk0gF6
yUWhrHnl8duSBHrcre4VnCrCA+Z90JMSduytC8PtE2tjyJC0rwGgCcucsNNS48Q4
391pOpTYY4bNlivYL4gJq34+ZgtI2Z3T3D9HlZJdjtgceCVOSwq8V31phQVz+k+L
4aP0s3HSSRZtYx91711eApaz22JfESWojBouHCSDo+zKDydtjDICLPxMsVl/PSNT
N3kui2sXKFyeVNGMjB37HlrO4C52C1ZCd6ckvR/PNRzDPAEjWNui9o7qjmXEVXHp
gRRvaSrDETs4d9NBFRzXlUpDDvuCPIlwYMYPZ+WGwsZy/mEmeWOw0VURkyLtveOc
nwoM0n/FrGMNnjJUbcezxaJQ73V0rPToXs1AluejYD139s3L0rP3H/TqgaOgEe/z
GQ7uCcWZFfCk6MprZKIJivKBa6/OeccowCluuQINBF3BfpwBEADYDy8UDuY2qRTe
/E5AVeL1sFgcvEsSrzDFj+5BpEEilFMhjDsp9oX5OKmPL4i8oRbtaBbBTzJ5UB06
wFilqD4xD9eZjDzMBWzOqTN0O0qrq7AFWF5i3Xh8hni11Ir8N7pgJFItNorM3nZA
wpB0+EDqy6K25I3QOwaJIUjkW9jx3W9Bl1u0SL6jNPW2msvd0+U2RYTEsPFeML2f
Nlavh0n/zG9erjh4dtSvdv6g/henFcLO59q0QGQNN0s3hKiqEkRQ4SlgIbFuDfeM
TyrBRI/SNYVOIKV9Ttht4eMJsHzQxGo1esimSve2jIKHtvBHcdQka97y7kEK6boM
El3nmF31tyDrpg1C95sdAaCym4kFK+lo9ApBgVEdjNZIn0TKCZ/uCcxgPVabI6s4
2TFDKVXyIGF8AOJL/oAYozEfa4tWkM6VO2x0ia+toPn0GrV6r5SeMBoss1jObdP5
nYIxhaYsVv2oDsyRuCNGs4j+7+MsWckjS0rkvKk/MG07sWepnKh/HbgYC+y+sFxl
5Ju+RqppXu8ErdEVI7ZmSBku+Uk3Y2Il8WS64c5/wIpJVTzvPV+Wui02QzsLYEQF
QUUjNEgYohrFpiShWmow1rHLemKyq780kIjd3yMjznL507SI0p0rrWqeeYDWeZjs
1a3bk5fhczYWmhlB02D4A2UMi4CFnQARAQABiQI2BBgBCgAgFiEE0uqPZ8baSeZk
9Jza1StNGVCoMcAFAl3BfpwCGwwACgkQ1StNGVCoMcBcdg/+NfbLREUkuHGKxDQU
gWEhjvXFfEuIsCmJcWhLCORjYB0lDc2kUcuuzz0t6xpzxjq577UBl92NcshL3BcZ
42qYPH31DQeQ1vQlJZjGVGcxmhuEJ6mKyu/8Ip9Lfhsf5OHfdjgir3E4EjS07Fo8
wHou+TwWin0OOE3K9e7HjL7yUct+STY8kun+I575hyn33NxiyLxwHNiKU6uUzdd3
Gh/DipSL6klOEFLP5R12iOn4PCDdzbIM3OTgRBUHs5ZMTlS6ZCvGiaVdzDHhYoCU
REUkx6yx6ficU64F5DaesArdeBw1NaCH4oJADis5Ss7Tn2vE+BzXkUqtXq/ZMReq
6+YcOyAd6d7l2gNk4FKB1bUap96UUOds8iw0yNsWl2Ie+QKrA5Z+UNoHcRS1VH4P
Exg9Bcxca6nNq4zC2FuzKocsaC8sBcqcq00R0CI/ZUKY6C5t+rYD/BTXB4hjpxY1
2rjjg2M7jAq+UmiOtjXPwxdv3ypGGVkEKGi0LbKYML7ldlMLxNlQyfcIQlnIXxaG
uu2hiUaEfGmE8ZX+iNLCMFaoSlbVagLAkw16ldj3Kkckw80lMxjCrFjEpV42N4wN
WmqPqLGdYcTEngPUo0zEuuIEYbAaWHxOmhEGZk0f3RQ7L0s5EdIeFtDN9XaOlTbb
oM5b6VLElyNwCqSgyjFL+MT29+0=
=RTzK
-----END PGP PUBLIC KEY BLOCK-----